2

2. Review of Two-Phase Critical Flow Models

For high-pressure systems, it is reasonable to assume that critical flow conditions exist at the rupture. The critical flow rate through the rupture can be predicted given the initial stagnation properties of the system, and, under certain condition, the subsequent pressure history can be predicted using this initial flow rate.

Critical flow is defined by the following differential equation :

(2-1)

and it corresponds to the maximum flow rate that can be achieved by a compressible fluid as it passes from a high-pressure region to a low pressure region. In many cases, a rupture’s flow behavior is modeled as a nozzle. Figure 2-1 shows a two-dimensional view of such a nozzle and its corresponding pressure behavior with respect to position. Any further reduction of the exit pressure below the critical pressure, , does not increase the flow rate through the nozzle. The maximum mass flux defined by Equation 2-1 corresponds to the throat of the nozzle, where the critical pressure ratio, , exists.

As an example, the isentropic single phase mass efflux, based upon ideal gas relations, from a ruptured system is derived as

(2-2)

where the subscript, , refers to stagnation properties of the fluid that correspond to a zero-velocity flow condition within the bulk fluid of the pressurized vessel . Unfortunately, the analysis for two-phase flows cannot use the ideal gas relations. Thus, other methods of analysis must be used to predict choked flow. In the past, many attempts to predict this flow condition have proved it to be an overwhelming task. Included below are some brief descriptions of the more widely used and recent two-phase flow models available.

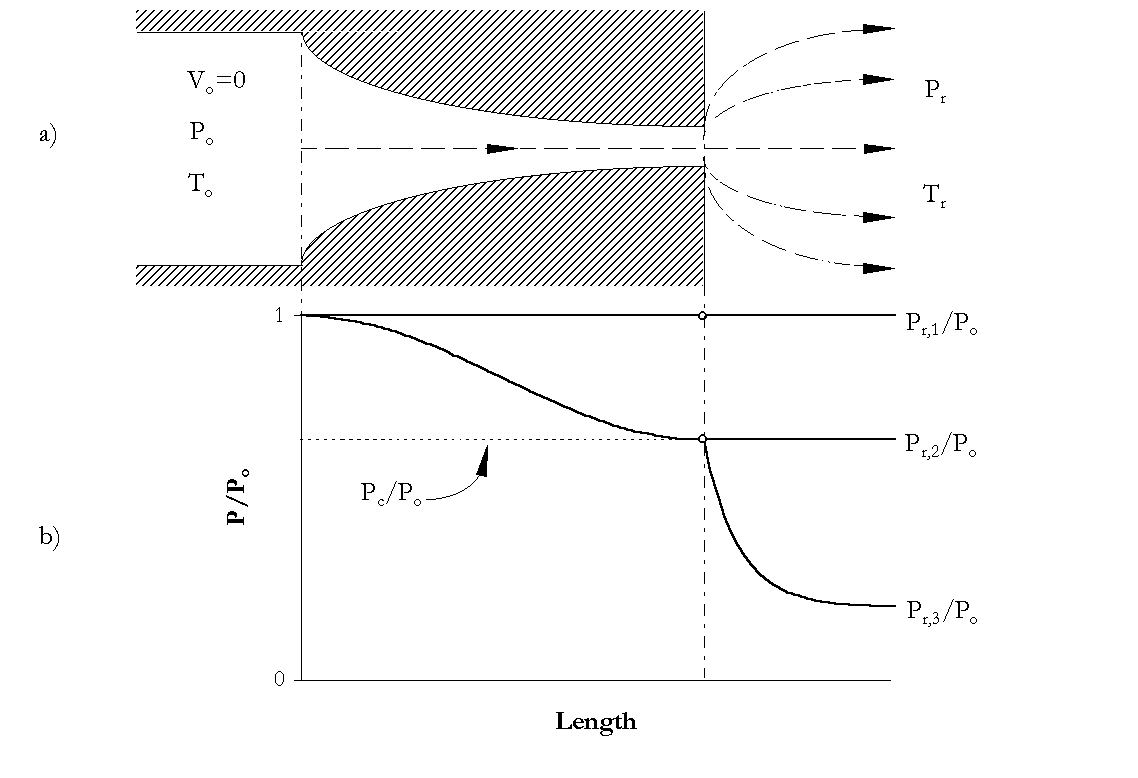
Figure 2-1. a) Generic converging nozzle diagram for the visualization of critical flow conditions. b) Typical variation in pressure as a function of position in a converging nozzle and of receiver pressure .

2.1 Homogeneous Equilibrium Model

One of the most widely used critical flow models is the Homogeneous Equilibrium Model (HEM) . This is primarily due to its simplicity. The HEM assumes there exists no difference between the liquid and vapor velocities within a continuum. Also, the two-phases are assumed to exist at the same temperature and pressure. This flow model is derived from the relationship between the mixture mass flux, density and velocity,

(2-3)

From the first law of thermodynamics, the stagnation enthalpy is shown to be related to the critical (see Equation 2-1) enthalpy and velocity by

(2-4)

Note this is a simple potential and kinetic energy balance for the fluid mixture. By assuming an isentropic expansion from the stagnation conditions to those at the critical point,

(2-5)

and by assuming saturated stagnation and critical conditions, a critical mixture quality is determined to be

(2-6)

The saturated values, and , are determined at the critical pressure, and is determined as the saturated liquid entropy, , at the stagnation pressure. Now, the expression for the mixture velocity, V, is determined from Equation 2-4 to be

(2-7)

and the enthalpy, , is calculated, using the saturated enthalpy values at the critical pressure, to be

(2-8)

Similarly, the mixture density can be determined at the critical pressure in terms of the liquid and vapor specific volumes,

(2-9)

Finally, incorporating Equations 2-7 through 2-9 into Equation 2-3 yields the following expression for the critical mass flux:

(2-10)

Figure 2-2 shows the typical dependence of mass flux as a function of the pressure ratio. By varying the local pressure, Equations 2-3, 2-4, 2-8, and 2-9 yield the curve shown for a chosen critical vapor quality. The critical flow condition occurs at the critical pressure ratio as shown. The HEM has been shown to be a good approximation for critical flow at high flow rates and high stagnation pressures in pipe lengths greater than 30 cm .

Figure 2-2. Typical variation in mass flow rate per unit area as a function of pressure ratio .

2.2 Equilibrium Rate Model

A superficial mass flux is defined as the phase-specific flow rate per unit cross-sectional flow area, or, for phase "k",

(2-11)

where , and are the area-averaged magnitudes of density, velocity and void fraction respectively. For a vapor-liquid mixture, the total mass flux is

(2-12)

(2-13)

If the liquid void fraction is stated in terms of the vapor void fraction,

(2-14)

and a homogeneous mixture is assumed (i.e., ), the mixture mass flux becomes that of Equation 2-3,

(2-15)

For a critical mass flow rate, , through a constant cross-sectional area, , the following relation can be obtained from Equation 2-15:

(2-16)

Rearranging Equation 2-16 yields

(2-17)

where the subscript, , refers to critical flow conditions. The single-dimension momentum equation in the "z" direction for a Newtonian, incompressible fluid is

(2-18)

By neglecting viscous and gravitational effects and by assuming a uniform flow mixture, Equation 2-18 becomes

(2-19)

(2-20)

Upon substitution of Equation 2-17 into Equation 2-20 and multiplying both sides of the resulting equation by ,

(2-21)

which simplifies, by using Equation 2-15 and canceling terms, to

(2-22)

Note that

(2-23)

which allows Equation 2-22 to become

(2-24)

(2-25)

Given the Maxwellian equation

(2-26)

and the assumption

(2-27)

where "sat" refers to saturated conditions and is an arbitrary function of volume, the following is obtained:

(2-28)

Integrating Equation 2-28 over the two-phase region yields

(2-29)

Given the relation

(2-30)

and noting that is constant in the two-phase (saturated) region, the equation

(2-31)

can be integrated over the two-phase region to yield

(2-32)

Equation 2-32 can be substituted into Equation 2-29 to obtain the Clausius-Clapeyron relation,

(2-33)

Now consider

(2-34)

and note that 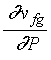is negligible, so that

(2-35)

If the stagnation conditions are assumed to be saturated and the expansion to be isentropic, Equation 2-35 becomes

(2-36)

By using Equations 2-33 and 2-25, it is apparent that

(2-37)

and

(2-38)

Equation 2-38 is the well known Equilibrium Rate Model (ERM) where and refer respectively to the latent heat of vaporization and the change in specific volume across the entire saturation line corresponding to an absolute saturated receiver temperature, . The specific heat of the saturated liquid, , corresponds to the same saturation temperature.

Hans Fauske proposed a modification of the ERM that is useful for the prediction of the non-equilibrium region, and produced the Relaxation Length Model (RLM). In this region the flow increases dramatically as the duct length decreases — approaching all liquid flow as the length approaches zero (i.e., orifice flow). The choked flow, , is defined by the following in the absence of significant friction losses:

(2-39)

The non-equilibrium number, N, , is defined by

(2-40)

where is the resistance coefficient and is the saturated liquid specific volume at temperature . Fauske determined a critical duct length, , to be 0.1 meters. As the duct length, approaches the critical length, the value of approaches a value of one, which corresponds to equilibrium flow conditions. When equals one, the above equation becomes the well-known ERM that has an alternate form,

(2-41)

Another variation of the RLM occurs when the duct length equals zero. This implies no flashing occurring through the break and the RLM equation simplifies to the well known Orifice Equation Model (OEM) for incompressible liquid flow as follows :

(2-42)

A comparison of the HEM, ERM and OEM (Figure 2-3) demonstrates the effect of an increasing duct length, , resulting in the choked flow approaching an asymptotic value corresponding to equilibrium flow conditions. In other words, the flow behavior is obviously less sensitive to an increase in the duct length when the critical length is reached.

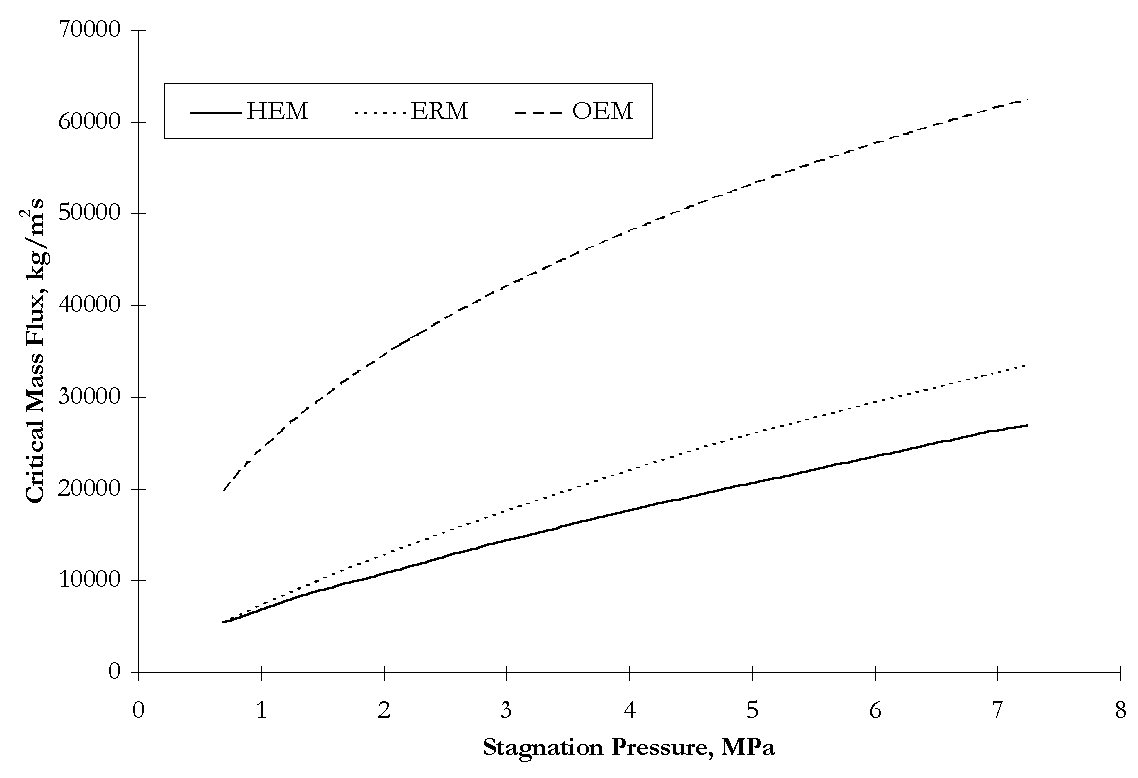
Figure 2-3. Critical mass flux for initially saturated water calculated by analytical models: Homogeneous Equilibrium Model, Equilibrium Rate Model, and Orifice Equation Model.

2.3 Low Flow Quality

Since its inception into the mainstream of two-phase critical flow analyses, the HEM has been shown to severely under-predict the experimental data for low vapor quality . Henry and Fauske developed the following transcendental expressions, often called the Henry-Fauske Subcooled Model (HFSM), for subcooled and saturated liquid stagnation conditions :

(2-43)

(2-44)

Experimental analysis yielded the approximation

(2-45)

The subscript, , refers to a fluid state in which the phases are in velocity, temperature and free-energy equilibrium. The conditions at the nozzle’s throat, denoted by the subscript , are considered to be at this equilibrium state. The HFSM predicts the data reasonably well throughout the reported ranges of pressures and subcoolings.