A Continuum Approach to the Modeling of
Microstructural Evolution in
Polycrystalline Solids
The diffusion of atoms from one region to another in the crystal lattice under the effect of stress is the underlying mechanism of several physical phenomena; e.g. void formation, grain-boundary movement, diffusional creep. It is the aim of this project to study this type of phenomena by modeling the underlying stress-driven self-diffusion mechanism in a computational setting.
When polycrystalline systems are considered, the computational cost of atom-by-atom modeling strategies becomes prohibitive. A continuum formulation which captures the atomic-scale physics is therefore adopted.
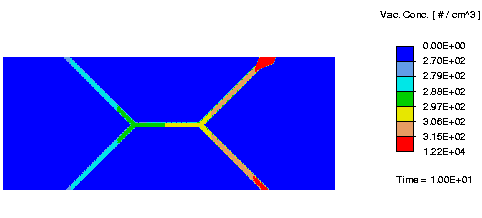
In this 1-micron wide Aluminum interconnect wire, the blue regions represent grains and the narrow colored regions represent grain boundaries. Atoms and vacancies diffuse under the effects of both stress and an applied electric potential difference, resulting in the shown vacancy concentration gradients. This animation (QuickTime | AVI) illustrates how the above gradients are developed, starting from a spatially uniform distribution of vacancies. Since the vacancy formation energy and the activation energy for diffusion are low in grain-boundary regions, vancancies diffuse faster and accumulate in these regions. Vacancies accumulate even faster at the upper-right end of the grain-boundary path where the formation energy is lowered further to model the effect of an impurity
Classical treatments do not address the fully coupled nature of the problem, but rather assume that the stress is imposed, i.e. the state of stress is known a priori. In the present formulation, the mechanics problem is solved for the stress at each time step, taking into consideration the influence of the composition on the state of stress. The composition problem is also solved for the vacancy concentration at each time step taking into consideration stress and electromigration effects.
On top of this formulation, an extension has been developed to study void nucleation within the context of classical nucleation theory. Another extension has been developed to make use of the Level-Set Method in modeling phenomena involving moving interfaces; e.g. grain-boundary migration and void evolution and growth. This animation (QuickTime | AVI) shows the evolution of the vacancy-concentration field in the presence of a migrating grain boundary. In addition, the formulation is currently being developed further to study morphological evolution of surfaces.